Entry 7:

Some common uses of similar triangles in real life range from nearly anything you can imagine, from trusses on houses, to sails on a sail boat. you can use this anytime something arises, and not just with triangles either! Let's say you own a sailboat,

Nice boat! but, lets say you need to buy a new sail,  the one you have ripped. So you order a new one online, but you get it, and it's too big!

Instead of returning it, because the company won't let you, you decide to cut it down to the proper size.

So, lets say that your sail is  6 feet tall, and 4 feet wide at the bottom.

So you take your sail, and measure a 4 foot wide base, and mark it, and go up on the altitude of the triangle six feet snd mark it. You knowbthat both triangles are righht triangles, and have an angle of 45 degrees. You make a lin going from the corner, to the six foot mark and cut it. that ins how you use similar triangles in a real life scenario!!

tips from pros unit 1

unit 1 day 8

Definition of Scale Factor

• The ratio of any two corresponding lengths in two similar geometric figures is called as Scale Factor.
• The ratio of the length of the scale drawing to the corresponding length of the actual object is called as Scale Factor

scale factor is where you want to find how much bigger the other object is and you do that by taking the bigger object number angle and dividing it by the smaller one such 

′
 once you divide it out, you get 1.5 and that means that the newer object is 1.5 times larger than the original.




Here's a practice quiz!

unit 1 day 6

Here, we are talking to you about angle angle. Angle angle is where you take 2 triangles and see if they're similar.

We do that by, taking 2 triangles--

Now we see that they are corespondent, a-e  b-g  c-f

lets say a-e are 75

and b-g are 69

now we have to find c-f

in order to do so, we take 180(because the total sum of a triangle's angles are 180) and then we take 180-75-69 and we end up with 36. that means that c and f are 36. When you add them up, 75+69+36 then you would get 180, in other words, you subtract 2 angles from 180 to get the third, and if both triangles have 2 equal degree of sides, then they are similar.

Here is a little practice quiz :

Is triangle PQR congruent to
            triangle STV by SAS? Explain.

Show that triangle BAP is congruent
              to triangle CDP.

  Problem 1Segment PQ is congruent
              to segment ST because
              PQ = ST = 4.
            Angle Q is congruent to
              angle T because
              angle Q = angle T = 100 degrees.
            Segment QR is congruent
              to segment TV because QR = TV = 5.
            Triangle PQR is congruent 

              

 Problem 2 Angle A is congruent to angle D
                  because they are both right angles.
               Segment AP is congruent to segment DP be-
                  cause both have measures of 5.
               Angle BPA and angle CPD are congruent be-
                  cause vertical angles are congruent.
               Triangle BAP is congruent to triangle CDP
                  by Angle-Side-Angle.

Unit 1:Entry 2
In this entry, we will go through what similar, and congruent shapes are, and the differences, and also how to find the area of similar/congruent shapes. We'll start by defining these terms, in "Math speak"

Similar Shapes:These are two or more shapes that are the same shape, just reduced or enlarged.

 Here is an example of two similar shapes.

Congruent shapes: these are two or more shapes that are exactly identical.


In this picture, all the side lengths on triangle ABC are equal to those on EDF. making them Congruent.

So, now that you have that out of the way, we're gonna work on finding the area of similar shapes, because congruent shapes are identical, their area/perimeter will be too!

For this example, lets use some similar triangles.
Similar triangles have the same shape, but they are scaled differently, so they may  be different sizes.
This is where you may need to use some base knowledge of proportions


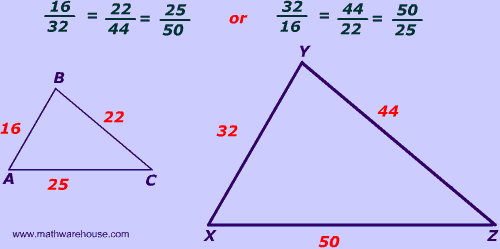
In this example the smaller triangle, is exactly 1/2 as big as the large one, this is made prevalent by the length markings on each leg of the shape.

Lets move on to a more in depth example
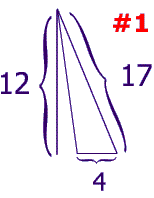
 A= 1/2 4*12=24

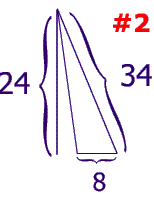
A=1/28*24=96
Notice, that 24/96 reduces too 1/4. you can see here that triangle 1 is 1/4 the size, or 4 times smaller than triangle 2. this is due to the similarity ratio, or scale factor.
now, you may be asking, how do you find the ratio?
all you have to do is pick to corresponding sides, and set it up as if it were a fraction, and then simplify it!
It's super simple, just as I demonstrated in the above problem!



Lets try some practice problems!
The key will be below.



In this triangle, A'C' is paralell to AC.  Find the length of B'C and  A'A





















 A research team wishes to determine the altitude of a mountain as follows: They use a light source at L, mounted on a structure of height 2 meters, to shine a beam of light through the top of a pole P' through the top of the mountain M'. The height of the pole is 20 meters. The distance between the altitude of the mountain and the pole is 1000 meters. The distance between the pole and the laser is 10 meters. We assume that the light source mount, the pole and the altitude of the mountain are in the same plane. Find the altitude h of the mountain. 










The two triangles are similar and the ratio of the lengths of their sides is equal to k: AB / A'B' = BC / B'C' = CA / C'A' = k. Find the ratio BH / B'H' of the lengths of the altitudes of the two triangles.  (NOTE: The altitude of a triangle is the height)




























_______________________________K E Y_____________________________________






Problem one:
First, use the proportionality of the lengths, to write an equation that helps solve for X and Y
(30 + x) / 30 = 22 / 14 = (y + 15) / y

The quation for X may be written like: (30+x)/30=22/14 = (Y+15) /y

Then you solve the above for X
420 + 14 x = 660 

x = 17.1 (rounded to one decimal place). 

The equation for Y may be written like:
22/14 =(y+15)/y
THen you solve the above, to get the answer: Y=26.25









Problem Two: 
First draw a horizontal line LM. PP' and MM' are vertical to the ground and therefore parallel to each other. Since PP' and MM' are parallel, the triangles LPP' and LMM' are similar. Hence the proportionality of the sides gives: 

1010 / 10 = (h - 2) / 18 
Then solve for H to get,: H=1820 meteres.


Problem Three:
If the two triangles are similar, the corresponding angles are 100% congruent, therefore the angles BAH and B'A'H' are exactly the same. These triangles have two pairs of corresponding congruent anges, BAH and B'A'H' and the right triangles BHA and B'H'A'. they are similiar, therefore; AB/ A'B'=BH/B'H'=k

UNIT 1-day 4

For instance, say you were an engineer putting up glass on the Luxor hotel in LAS VEGAS.
It is a 3-d pyramid and you are the leader for how big the hotel is.

to find the total surface area, you are to take the base of the luxor. The base is 646ft. Then, you are to find the slant height which is 476ft. to find the total surface area,  it's 2bs+b2
so that means, you take the base length and multiply it by the slant height. after you do that, you multiply it by 2.
it should look like--
646ft x 476ft=307,496 x 2=614,992

after that, you take the base and square it. 646ft(2)  and that gets you__360,000

after the 2 numbers are acheived, you add them. 360,000+614,992= 974,992ft 2**total surface area***                                                            ^^^^^^



quiz

A-a pyramid has the base of 120ft and the height of 300ft, what is the surface area?
B- a cylinder has a height of 10ft and a radius of 50ft, what is the surface area?
C- a prism has a base of 300ft and height of 27ft, what is surface area?

answers



A-259,200ft2
B-17,584ft2
C-8100ft2

Entry:5
In thie entry, we're gonna touch on  how to find the missing lengths of a similar triangle. If you remember from entry 2, Similar triangles have the same shape, but they are scaled differently, so they may  be different sizes.
This is where you may need to use some base knowledge of proportions.
You can use proportions to figure out the side length.

If a triangle has a height of 12, length of 2 and hypoteneuse of 24
and a similar triangle has a height of 24, length of 4, but the  length of the hypotenuse isn't given, you can set up a ratio.
12/24
6/12
3/6
1/2
so the triangle is  1 half of the size as the larger one.
you can do this with any triangle, as long as at least one side length on each shape is given, then you can set up a ratio,  and work from there, getting the ratio, simplifying it and coming up with the fraction; whatever it may be


                                            Lets do a practice quiz!

On a sunny day, Michelle and Nancy noticed that their shadows were different lengths. Nancy measured Michelle's shadow and found that it was 96 inches long. Michelle then measured Nancy's shadow and found that it was 102 inches long.

a.	Who do you think is taller, Nancy or Michelle? Why?
b.	If Michelle is 5 feet 4 inches tall, how tall is Nancy?
c.	If Nancy is 5 feet 4 inches tall, how tall is Michelle?

Nancy is taller. Since the right triangles defined by their heights and their shadows are similar, then the bases of the triangles have to be proportional to the heights of the triangles (i.e., their body heights).

b. 

Converting Michelle's height into inches (64 inches) and setting up a proportion, you would have:

64 / x = 96 / 102, or

x = 68 

Converting 68 inches back to feet, Nancy is 5 feet 8 inches tall.

c. 

Converting Nancy's height into inches (64 inches) and setting up a proportion, you would have:

64 / x = 102 / 96, or

x = 60.24

Converting 60.24 inches back to feet, Michelle is approximately 5 feet and 1/4 inch tall.

UNIT 1 day 3

-Suface Area-

 Surface area is the total area of the surface of a three-dimensional object.

(surface area examples)

Surface Area of a Cylinder = 2 pi r ² + 2 pi r h

The surface area of a prism = 2 × area of base  +  perimeter of base × H

Pyramid-[Base Area] + ¹/₂ × Perimeter × [Slant Length]

Cone-SA = πr² + πrl

Surface Area of a Sphere = 4 pi r ²

an example of when we would use surface area, is anytime we need to know how much of something will fit into a 3-d figure, such as being a plumber. They need to measure pipes and find the surface rea and volume to know how much water can and will fit. Or also when they checked out the pyramids, they needed to use surface area to know the overall size. Surface area is hugely used in engineering as well.



Here's a practice quiz!
Calculate all surface areas























KEY





Problem one:

For both the front and back faces, l = 5 in. and w = 2 in.

So, the area of the front and back faces is,

5  2  2 = 20 in.²

For both the top and bottom faces, l = 14 in. and w = 5 in.

So, the area of the top and bottom faces is,

14  5  2 = 140 in.²

For both the sides, l = 14 in. and w = 2 in.

So, the area of the two sides is,

14  2  2 = 56 in.²

Add the area of the faces.

20 + 140 + 56 = 216

So, the total surface area of the given solid is 216 in.².

Problem 2:

The triangular prism has triangular bases.

So, to find the area of the bases, use the formula:

Substitute 6 for b and 8 for h.

Therefore, the area of the two bases is,

2(24) = 48 cm²

The triangular prism has rectangular sides.

So, use the formula A = lw to find the area of the sides.

The area of the front side is,

13  8 = 104 cm²

The area of the bottom side is,

13  10 = 130 cm²

The area of the back side is,

13  6 = 78 cm²

Find the sum of the base areas and the area of the sides.

48 + 104 + 130 + 78 = 360

So, the total surface area of the given solid is 360 cm².

Problem three:

The area of the curved surface of a circular cylinder of base radius r and height h is 2πr ·h.

Here, r = 4 and h = 16¹/₆. So, the area of the curved surface is,

2 ·π· 4 · 16¹/₆

To simplify, first write the mixed number as a fraction.

2 ·π· 4 · 16¹/₆ = 2 ·π· 4 ·⁹⁷/₆

Now, multiply.

2 ·π· 4 ·⁹⁷/₆ approx 406.3

So, the area of the curved surface is about 406.3 in.².

he cylinder has circular bases.

So, the area of each base is πr².

Here, r = 4. Therefore, the area of the two bases is,

2(π· 4²)

Simplify.

2 ·π· 4² = 2 ·π· 16  100.5

Add the area of the bases to the area of the curved surface.

406.3 + 100.5 = 506.8

So, the surface area of the given solid is about 506.8 in.

UNIT 1--day 1

In this Blog entry, we will teach you how to find the area of a square, rectangle, triangle, trapezoid, parallelogram, circle and a polygon. Also, we will define what a point, a line, segment, ray, angle, median, altitude and perpendicular, along with some practical application.

The area formulas are as follows:

Square:
A^2 where "A" is a side length.

Triangle:
1/2 (b x h)
B= base length
H= height

Rectangle:
W x H
W= width
H= height

Circle:
3.14 x  r^2
R=radius

Parallelogram
B x H

Trapezoid:
 1/2 (a+b) x H
A= side length one
B= side length two
H= height

Polygon
 1/2 (apothem) (perimeter)

Also, we need to define...

Point:A point is an exact position or location on a plane surface. It is important to understand that a point is not a thing, but a place.

Line: A straight slope showing either growth, decline or constancy on a graph. extends infinently from both sides

Plane: A 2 dimensional figure

Line Segment: A part of a line with two dots on either end, sectioning off a part of a line, finite distance

Ray: a line that extends infinently in one direction

Angle: A shape created by two lines or rays diverging from a common point

Median: the middle

Altitude: otherwise known as the height of a triangle.


Perpendicular: A line is perpendicular to another if it meets or crosses it at right angles (90°). 








QUIZ
A- a triangle has a base of 5 and a height of 2, what is the area?
B- a circle has a radius of 20, what is the circumference?
C- a parallelogram is 30 by 20ft, what is the area?








answers
A-area is 5ft2
B- 396.6ft2
C- 50ft2 

DAY 6 -find an equation of a line with two points-

-find an equation of a line with two points-
basically stating, find a y=mx+b equation with 2 points
refer to entry 2, but in a real life setting

Here I have a price per amount in a bag full of paintballs.
I have 2 points that are (100,$4.00)
and I have ( 400,$14)
so i take the 400 and 14 and I simplify 400,14 so it equals 200 and 7
I divide the 200/7
and that equals+28.5


After its in the form
y=28.6x+b
I take the number 100 and $4


I add the Y to the Y=
and i add the X to the X

$4=28.5(100)=b

after i do the equation is should be
4=2850+b

Then i subtract the 4-2850 and that gives me -2846

so stating, they charge 28.46$ without purchasing any paint and just for advirtisement.

Entry:5
         In order to graph a linear equation, we can use the slope and Y intercept to graph it, and visually show the data the formula states.
For this example, we have a formula of: Y=1/2x+4


One way to graph it, is using the X and Y values of two points that satisfy the equation, plot each point and then draw a line through the points. You can start with any two x values you want, and then find "y" for each ''x''  by substituting the ''x'' values into the equations, Try it with X=1
If the value of x is one, and the formula is Y=1/2x+4, you should have written down "Y=1/2*1+2=1/2+2" Which then gives you a value of Y, which, after solving should be 2.5. 
The "B" value in the equation can be used a start point for your graph, and then you can use rise over run to graph the lines.















You can also work backwords to find the equation from a graphed line,
Let's Practice

tip from pros-line of best fit

Day 4: define Y intercept and "real world meaning"

Entry 4
Define the "Y" intercept


The y intercept is where the the line of the equation crosses the y axis.

As you can see, the Y intercept is the point at (0,0). Basically saying, in real life, the Y intercept in this meaning would mean, if you didnt do your homework, then, you get a 0 on your math test. And if you increase the Y intercept, it means that's your test score, based on the amount of homework that's been completed.




Know that you know the dictionary definition of the Y intercept, lets practice. Here are a few graphs.

Use the Red line only













ANSWERS:
Graph 1: The Y intercept is (0,3)
Graph 2: The Y intercept is (0,18)
Graph 3: They Y intercept is (0,1)

Entry 2: How to find linear equations.
Linear equations are, simply the Y=Mx+b formula for graphing a line. This is commonly referred  to as he slope intercept form, because the equations states both the slope and the Y intercept.
The "M" gives the slope, and the "B" gives the "Y" intercept.
Here's an example:

• Find the equation of the straight line that has slope m = 4
  and passes through the point (–1, –6).

In this instance, they have given you the value of the slope. Specifically, "M=4". So at this poin, you can plug that into the equation as: Y=4x+b

They have also given you an X and Y value, -1 and -6 respectively. In the slope intercept form of a straight line, You have Y, M, X and B, all you need to do now is plug in what they have given you for the slope and the X,Y from the given point, and solve for B. like this:

Y=mx+b

(-6)=(4)(-1)+b

-6=-4+b

-2=b

 Congratulations! You just found the linear equation!! But what if they don't give you the slope?

Find the equation of a line that passes through the points (-2,4) (1,2) 

Well,this is where you would use the slope formula! The slope formula is an easy method to find the slope of a line.

If you have two points on a straight line, you can always, ALWAYS find the slope with this method.

     

After plugging in and solving, the slope you should have gotten is -2/3

Now that you have the slope AND two points,you can solve for the equation. Lets use point (-2,4)

Y=mx+b

4=(2/3) -(2)+b

4=4/3+b

12/3-4/3=b

B=8/3

So, y=(-2,3)x+8/3

The answer is the same no matter which point you use. Now lets practice!

With this equation Y=5/3x+2, graph the line using the same method above.

This should have been simple, because you have the full equation, and all you need to do is graph it.

Entry: 1
Line of best fit.
Here in this blog entry, we will show you how to properly find the line of best fit.
Firstly, You need your data points, preferably set up in a nice chart like this:

Sandwich	Total Fat (g)	Total Calories
Hamburger	9	260
Cheeseburger	13	320
Quarter Pounder	21	420
Quarter Pounder with Cheese	30	530
Big Mac	31	560
Arch Sandwich Special	31	550
Arch Special with Bacon	34	590
Crispy Chicken	25	500
Fish Fillet	28	560
Grilled Chicken	20	440
Grilled Chicken Light	5	300

Then, You can prepare a scatter plot of the points. In this demonstration, a piece of spaghetti was used to create the straight line, like so.



After that, you should pick the two best points that follow the trend of all the points and set the spaghetti, or best fit line, through them.



For this example, I chose points (9,260) (30,530)
You then can calculate the slope through your two points, like this
. (Note the answer in this image was rounded to the third decimal place, and is usually unnecessary )
You are then able to write the equation of a line!

You can now predict how the line would continue to grow, good job!

Here is a small practice quiz, to help you out if you feel like you need some extra practice the key is below:

The following table describes data for the number of people using a swimming pool over 8 days in summer and the corresponding maximum temperature (in degrees Celsius) on each day.




a.  Draw a scatterplot for this set of data.
b.  Draw a line of best fit through the data by eye.
c.  Is association positive or negative?
d.  Is association weak or strong?
e.  Use the line of best fit to predict the swimming pool attendance where the daily maximum temperature is:
(i)  18 ºC          (ii)  30 ºC           (iii)  40 ºC
































  The scatterplot is obtained by plotting y against x, as shown below.

b.  A line of best fit by eye is drawn through the scatterplot so that an equal number of points lie on either side of the line and/or the sum of the distances of the points above the line are roughly equal to the sum of the distances below the line.
c.  It is clear that y increases as x increases. So, the association between the variables is positive.
d.  The data is spread about the line. So, the association between the variables is weak.
e.
(i)  When x = 18, y = 260
     So, about 260 people are expected to attend the swimming pool.
(ii)  When x = 30, y = 400
      So, about 400 people are expected to attend the swimming pool.
(iii)  When x = 40, y = 520
       So, about 520 people are expected to attend the swimming pool.

Greetings!

Nick Kaufman

Hey guys, I hope the house turns out great and i hope you can enjoy for years to come! Blood sweat and tears have been put into making the house and it has been a big experience! The house was something new for me and it was great because i love building. Working with my hands is something fun I like, but also gives you a creative edge. I also enjoy playing paintball, snowboarding, listening to rock and dubstep, playing video games, Internet, and hanging with my buds and the girl friend.

 I learned a lot from this class, such as how to build a little house and teamwork. Meeting new people has been fun, and you get to truly see how people work or help or how lazy they can be. You should always help one another through anything, The math side hasn't been the greatest but if you can understand it, then helping you build a house has been a great eye opener. To me, u meet every kind of character in life. And for me, I like people who just like to get the job done without any slacking until everything is finished. You should always try and be the one to over achieve in life. sometimes things just turn out how you wanted. Always keep that goal mindset, if anyone says that's stupid or gets in your way, then you keep on doing what your passion is and knock em down. 

I liked working with you a lot Rob, because your a little high schooler at heart in a grown mans body! It doesn't hurt to be childish because you can always have the best times. An important lesson that was taught to me was family values. You have to always be there for one another and you have to work hard through tough times and never stop losing hope. For me to you, I wish you two the best of luck and hope that house can be the start and foundation of your family. I will write my name somewhere in that house and you can have a scavenger hunt to find it.